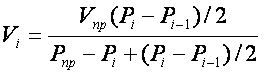Нелинейность деформирования оснований при работе ленточных и столбчатых фундаментов

Необходимо определить, чем обусловлена нелинейность на графике S=S(P_i) при работе нагруженного основания?

Данная нелинейность вызвана, прежде всего, появлением пластических деформаций, τ_z в основании, которые при Р_н.кр.равны 0, а при Р_i=R, τ_Z=(1/4)b.

Построим функциональную зависимость V=V(P_i) (см. рисунок) в координатах прикладываемого давления Р_i и объема зон пластических деформаций V_i, образующихся под подошвой фундамента. При построении данной зависимости необходимо исходить из следующих положений:

1. При достижении для фундамента заданных размеров давления равного начальному критическому Р_н.кр., объем зон пластических деформаций равен нулю (момент их зарождения).

2. При достижении для фундамента заданных размеров предельного давления на основание Р_пр, объем зон пластических деформаций также достигнет предельного значения V_пр. Это состояние на графике V=V(P_i) будет определяться точкой М (см. рисунок) положение которой в общем случае не определено.

Следует отметить, что проявление пластических деформаций в нагруженном основании зависит от ориентации рассматриваемого сечения, траектории и степени нагружения и др. факторов. Поэтому рассматривая слой грунта под подошвой фундамента как совокупность отдельных сечений, траектории изменения объема зон пластических деформаций этого слоя, для заданных размеров фундамента, при стремлении к точке М, можно придать наиболее вероятностный характер.

При этом допускается, что при изменении давления от 0 до R (точка 2) грунт практически во всем основании работает в линейно-де­фор­ми­ру­емой­ стадии, и поэтому «V» будет линейно зависеть от прикладываемого давления.

Примем ординату V₀ объема зон пластических деформаций, соответствующую давлению R.

Дальнейшее возрастание давления p_i > R, приводит к нелинейному увеличению объема зон пластических деформаций и, таким образом, к более интенсивному возрастанию ординат V_i по сравнению с V₀ (при p_i = R).

Соединяя последовательно единым вектором вершины названных ординат в интервалах давления ∆P_i, получим расчетную кусочно-линейную траекторию изменения объема зон пластических деформаций (а) в основании под фундаментом заданного размера (см. рисунок).

Тогда:

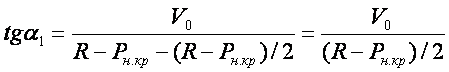
или

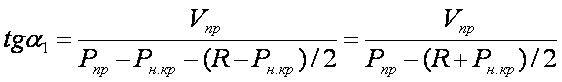
Приравнивая правые части выражений, получим:

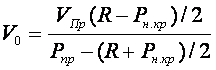
Поступая аналогично, можно записать:

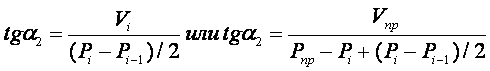
Приравнивая правые части выражений, получим: